Probability Distributions with Application in Textile Practice

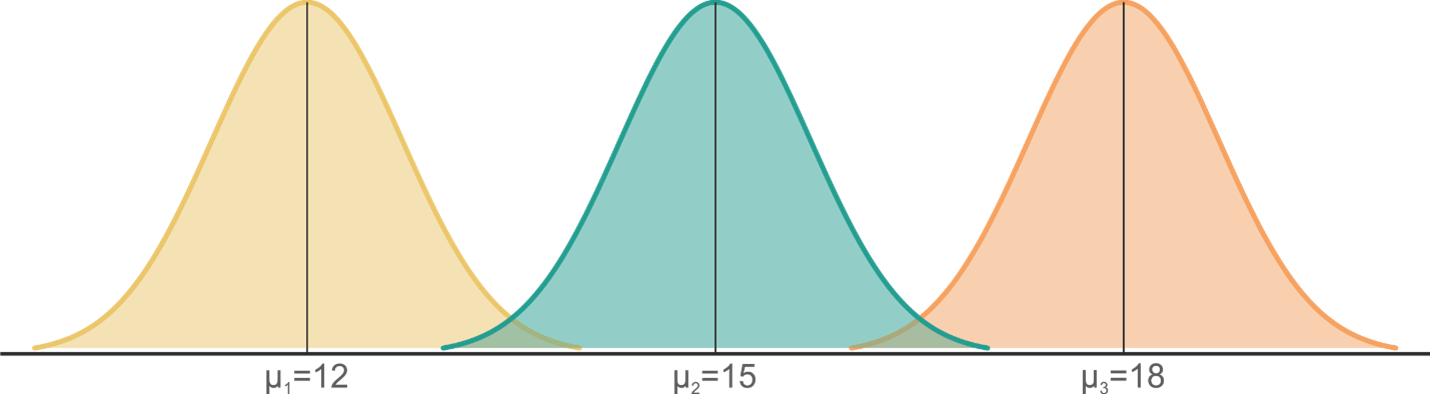
The standard deviation characterizes the spread of the normal distribution (Fig. 5.13):

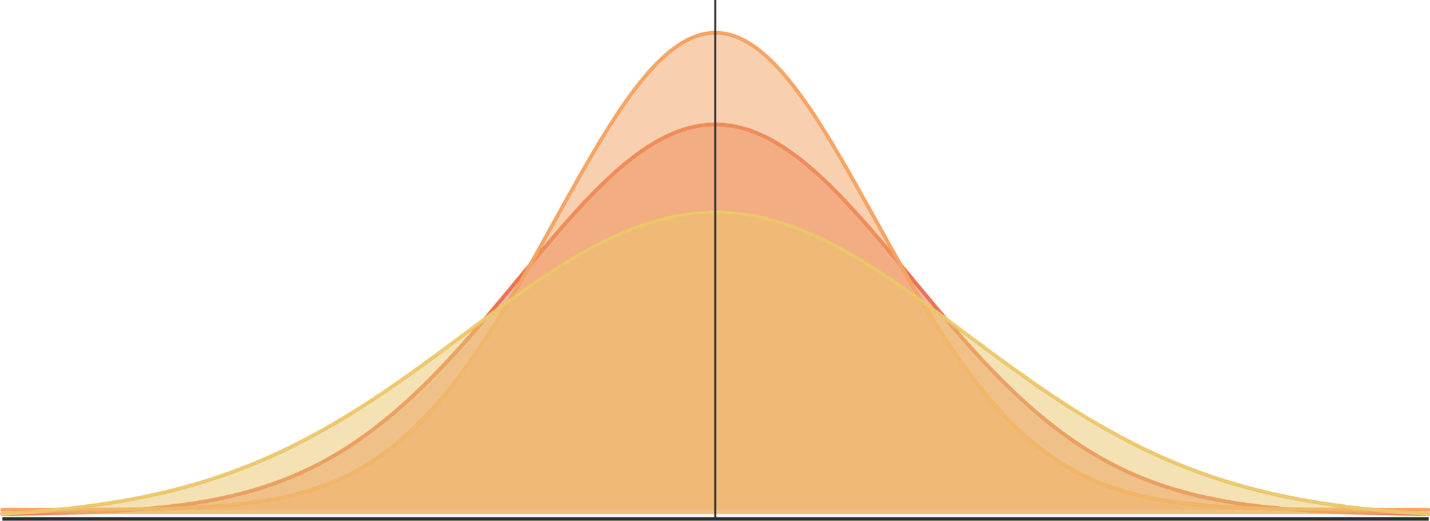
Fig. 5.13 Distributions with same mean, but different standard deviation

The larger standard deviation means larger spread, and the smaller standard deviation means smaller spread. When the spread increases the curve get much flatter, and when the spread decreases the curve get taller. The reason is that the normal distribution is a density curve, and the area below the curve is always equal to 1.

68-95-99.7 Rule

A survey shows that the average time of making jeans in an jeans factory is about 15 minutes, but it can be longer or shorter, depending on different factors. An experiment shows that the time is normally distributed with mean 15 and standard deviation 0.5.

This distribution can be defined as Normal distribution with \( \mu \) = 15 minutes and \( \sigma \) = 0.5 minutes. According to this data, we can construct a normal distribution (Fig. 5.14):

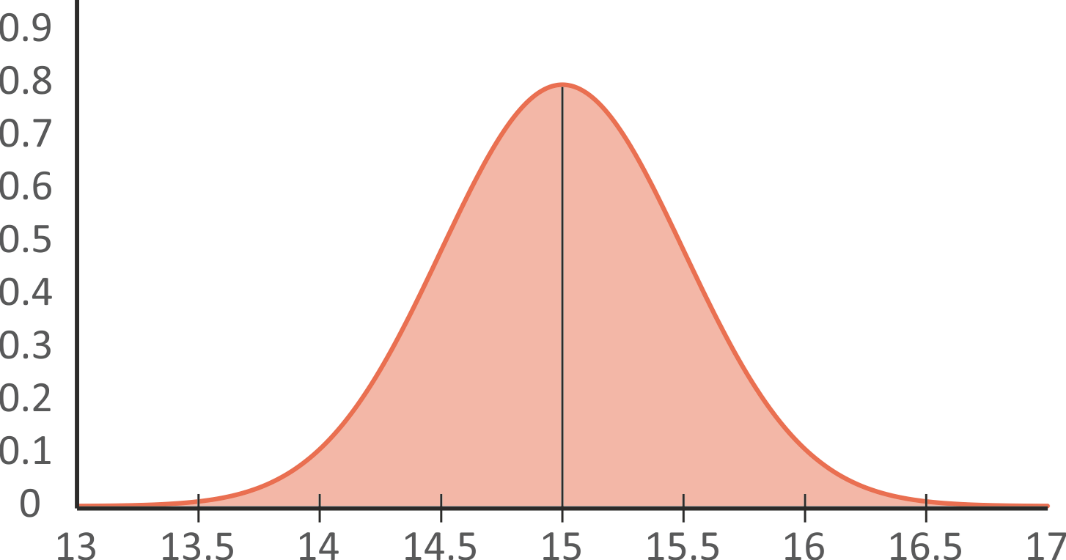
Fig. 5.14 Normal distribution with \( \mu \) = 15 and \( \sigma \) = 0.5

From the probability density function, you can see the time of making jeans is most likely 15 minutes, probably quite unlikely the time is 13 minutes or 17 minutes, but there is still likelihood in these eventual times.

The intervals on the \( x \) axis increase by the standard deviation:  15.5, 16.0 and 16.5, on the other side of the mean: 14.5, 14.0 and 13.5.

Fig. 5.15 Graphical representation of the 68-95-99.7 Rule of normal distribution with \( \mu \) = 15 and \( \sigma \) = 0.5

According to the 68-95-99.7 Rule (Fig. 5.15) one standard deviation away from the mean, it contains an area of 0.68. In this case 68% of jeans are made in the interval between 14.5 and 15.5 minutes.

If we go two standard deviations away from the mean, it contains an area of 0.95. In this case the time elapsed for production of 95% of the jeans is between 14 and 16 minutes.

If we go tree standard deviations away from the mean, the area is 0.997. This means the elapsed time for production of the 99.7% of the jeans is between 13.5 and 16.5 minutes.

The 68-95-99.7 Rule works for all normal distributions, no matter what shape and size (mean and sigma).

Example 1:

The normal distribution on Fig. 5.16 has a standard deviation of 10. What is the approximate area between 50 and 70?

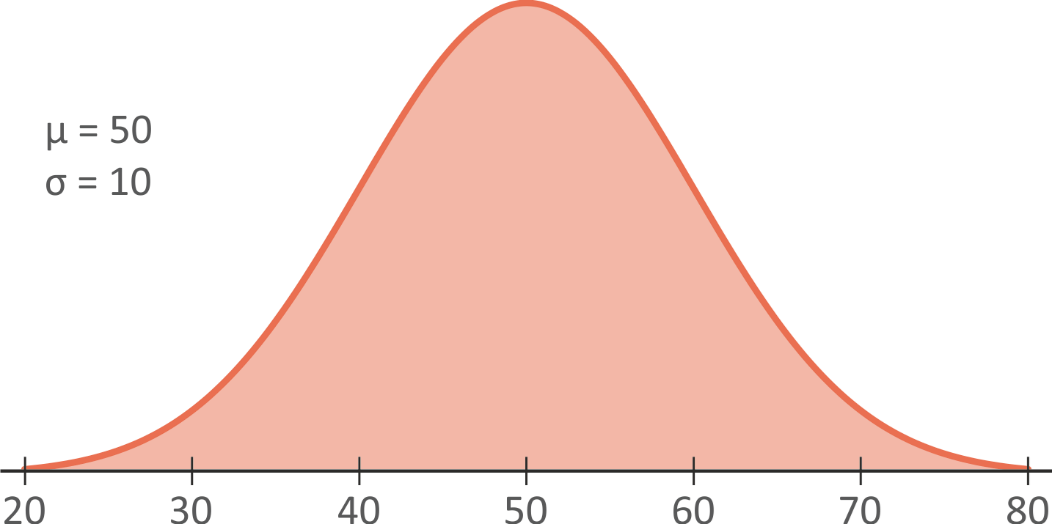
Fig. 5.16 Normal distribution with mean 50 and standard deviation 10

According to the 68-95-99.7 Rule there is an area of 95% between two standard deviations from the mean. Two standard deviations to the right gives us 70 and two standard deviations to the left gives us 30. So, the area between 30 and 70 is 95% (Fig. 5.17). We are interested in the area between 50 and 70, so dividing the area from 30 to 70 by 2 will give us the area of interest: 95/2 = 47.5%.

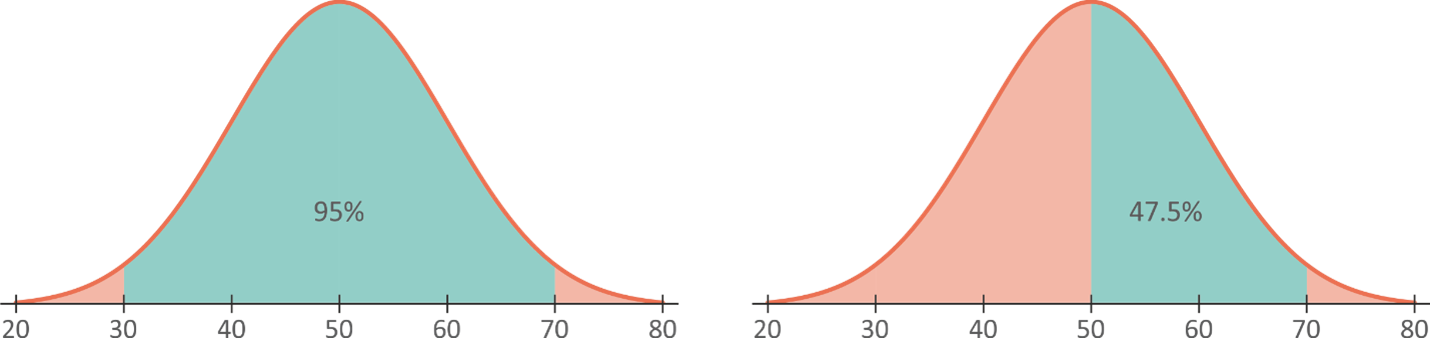
Fig. 5.17 Graphical representation of the 68-95-99.7 Rule of normal distribution with \( \mu \) = 50 and \( \sigma \) = 10

The approximate area between 50 and 70 is 47.5%.

Example 2:

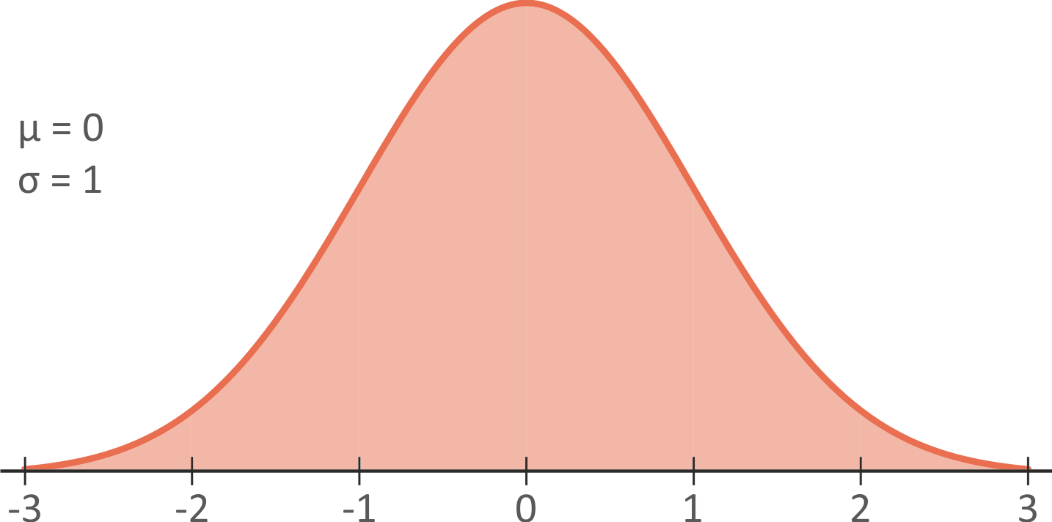
For approximation of the area between -2 and 1 we can use the 68-95-99.7 Rule (Fig. 5.19):

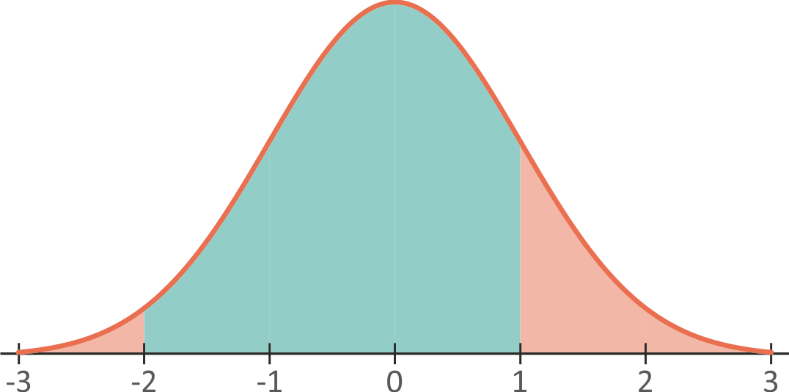
Fig. 5.19 The area between -2 and 1 on a normal distribution with mean 0 and standard deviation 1

If we divide this area into two parts (from -2 to 0 and from 0 to 1), we can easily apply the rule (Fig. 5.20):

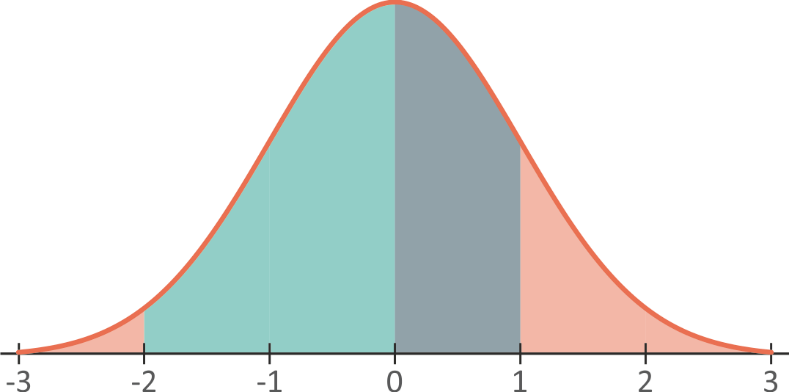
Fig. 5.20 The area between -2 and 1 divided into two parts

Let’s start with the left part which goes from -2 to 0. We know that two standard deviations away from the mean gives 95% and half of this is 47,5% (Fig. 5.21):

Fig. 5.21 Application of the 68-95-99.7 Rule

The next one is the right part which goes from 0 to 1. We know that one standard deviation away from the mean gives 68% and half of this is 34% (Fig. 5.22):

Finally, to get the area between -1 and 2 we must add these two areas together (5.23):

Fig. 5.23 Sum of the extracted areas

The area between -2 and 1 is approximately 81.5%